Triángulos isósceles

Para calcular un triángulo isósceles dados dos lados iguales ab y un ángulo contiguo g a uno de ellos a, se toma el vértice de uno de los dos segmentos como centro de la circunferencia, siendo el radio el mismo segmento a. Se coloca el ángulo g a partir del extremo del segmento y donde corta a la circunferencia la prolongación de su lado r obtenemos el vértice opuesto del triángulo.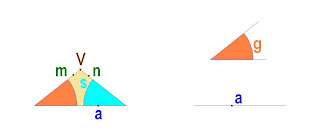

Para calcular el triángulo isósceles teniendo como datos uno de los dos ángulos iguales g (en color naranja) y la base a o segmento desigual del triángulo, se hace el ángulo simétrico del dado, la prolongación de los dos lados superiores m n de los ángulos dados genera el vértice superior V del triángulo.






Para calcular un triángulo isósceles dado uno de los lados a y el ángulo desigual g, basta con hacer una circunferencia c tomando como centro el vértice P del ángulo g y tomando como radio el lado a del triángulo. La intersección de la circunferencia c con la prolongación del otro lado simétrico del triángulo genera el vértice T que falta del triángulo.

Para calcular un triángulo isósceles dados dos lados desiguales ab, hacemos un segmento vertical c por el punto medio de uno de ellos a y tomando el extremo de este segmento M y la longitud del otro b hacemos un arco hasta que corte al segmento vertical c en el punto P que es el nuevo vértice del triángulo.

Para calcular un triángulo isósceles dado el lado a y el ángulo opuesto g, se hace por el punto medio del lado dado a un segmento perpendicular al mismo y se centra sobre un punto aleatorio P de éste el ángulo dado, de manera que la perpendicular sea la bisectriz del ángulo dado g. Haciendo por los extremos del segmento MN rectas paralelas zx a las del ángulo dado obtenemos en su intersección el vértice superior v del triángulo.

Para calcular un triángulo isósceles dado el lado a y el ángulo opuesto g podemos utilizar el arco capaz.

Colocamos en la base del ladoa el ángulo dado g y hacemos por el vértice del segmento a una recta perpendicular p hasta que corte en O a la perpendicular m por el punto medio al segmento a. Todos los triángulos que tengan como vértice un punto de la circunferencia y el segmento dado tienen el mismo ángulo g, según el arco capaz pero sólo dos son isósceles, a saber, los que corresponden a la intersección de la recta m con la circunferencia.

Para calcular un triángulo isósceles m dado el ángulo desigual g y la suma s de la altura más la base, dibujamos un triángulo isósceles cualquiera con ese ángulo g y teniendo en cuenta que todos los triángulos isósceles que tienen el mismo ángulo desigual g son todos proporcionales, transformamos la base b en un segmento vertical b' mediante dos circunferencias. A continuación aplicamos una homotecia o cambio de escala de manera que alineamos la longitud total del segmento que es suma de los dos con la longitud total que acabamos de calcular, todos los puntos están alineados.

En el dibujo las dos bases de los triángulos aparecen alineadas, casualidad altamente improbable a la hora de resolver el ejercicio.