Un triángulo es una figura plana formada por tres rectas a las que se les llama lados. Cada par de lados forman un ángulo, la suma de los tres ángulos del triángulo es 180°.
En un triángulo cada lado es menor que la suma de los otros dos lados y mayor que la diferencia.
Clasificación: un triángulo escaleno tiene todos sus lados y ángulos desiguales, el equilátero los tiene todos iguales, y el isósceles tiene dos lados y dos ángulos iguales.
Respecto a los ángulos, los triángulos se clasifican en acutángulos si sus tres ángulos son agudos (menores de 90°), son rectángulos cuando tienen un ángulo recto (de 90°) y son obtusángulos cuando uno de sus ángulos es obtuso (que quiere decir que tiene un ángulo mayor de 90°).
Elementos de un triángulo:
La mediatriz es la recta perpendicular en el punto medio del lado del triángulo. Las tres mediatrices del triángulo se cortan en un punto llamado circuncentro.
La mediana de cada lado es la recta que une un vértice del triángulo con el punto medio del lado opuesto. Las tres medianas del triángulo se cortan en un punto de intersección llamado baricentro.
La bisectriz de un ángulo es la recta que divide al mismo en dos partes iguales. La intersección de las tres bisectrices del triángulo es un punto llamado incentro.
La altura de un triángulo es la recta perpendicular desde un vértice del triángulo al lado opuesto. La intersección de las tres alturas del triángulo es un punto llamado ortocentro.

Un triángulo genérico o escaleno es aquel que tiene los tres lados y ángulos desiguales.
Para calcular un triángulo dados dos lados ab y un ángulo adyacente g a uno de ellos, se prolonga el lado del ángulo no adyacente hasta que corte al arco que define el otro lado b, tomando como centro N de ese arco el punto de intersección de los extremos de los cementos lados a b. El ejercicio tiene dos soluciones ya que la prolongación del lado que hay que calcular por el punto M intercepta a la circunferencia en dos puntos P O, que son los dos posibles vértices de los nuevos triángulos.
Para calcular un triángulo cualquiera dados sus dos lados a b y el ángulo g comprendido entre ellos basta con unir los extremos de los segmentos dados obteniendo el nuevo lado c del triángulo.
Para construir un triángulo escaleno dados un lado a y los dos ángulos adyacentes, se prolongan éstos hasta que se cortan en un punto P obteniendo de esta forma el triángulo.
 Para calcular un triángulo cualquiera dados sus tres lados abc, a partir de los extremos PS de uno de los lados a colocamos los otros dos bc y haciendo centro en los extremos PS y tomando como radio la dimensión a b de los mismos hacemos dos arcos hasta que se corten en un punto Ñ que es el vértice del triángulo.
Para calcular un triángulo cualquiera dados sus tres lados abc, a partir de los extremos PS de uno de los lados a colocamos los otros dos bc y haciendo centro en los extremos PS y tomando como radio la dimensión a b de los mismos hacemos dos arcos hasta que se corten en un punto Ñ que es el vértice del triángulo.Teorema: si inscribimos un triángulo cualquiera en una circunferencia y calculamos su ortocentro, los puntos simétricos del ortocentro respecto a cada uno de los lados del triángulo son siempre tres puntos que están sobre la circunferencia circunscrita.
http://teoremas-de-geometria.blogspot.com.es
Simétricos del ortocentro |
Nos dan las dos alturas que son los dos segmentos verticales verde y marrón, y nos dan
el lado del triángulo que es la base del mismo de color naranja.
el lado del triángulo que es la base del mismo de color naranja.
Las alturas las denomino g i, de 6 y 5 unidades , mientras que el lado de la base se le
llama f y tiene 8 unidades.
llama f y tiene 8 unidades.
Hacemos por el extremo superior del segmento verde - punto C- una línea horizontal h,
esa línea va a ser la que define la altura del triángulo y sabemos que su vértice superior H
va a pasar sobre esa recta.
esa línea va a ser la que define la altura del triángulo y sabemos que su vértice superior H
va a pasar sobre esa recta.
Hacemos centro en el origen A de coordenadas y con radio i, giramos el segmento marrón i
hasta que corte en el punto G a una semicircunferencia c construida sobre la base f del triángulo.
hasta que corte en el punto G a una semicircunferencia c construida sobre la base f del triángulo.
Construimos la recta que pasa por GB y la prolongamos hasta que corte a la línea horizontal h,
en el punto H, que es el vértice superior del triángulo, con lo que queda resuelto el ejercicio.
en el punto H, que es el vértice superior del triángulo, con lo que queda resuelto el ejercicio.
Fundamento: se basa en que la línea I y el segmento BG forman 90 grados por estar dentro
de una semicircunferencia, con lo cual el segmento I será una altura del triángulo ya que es
perpendicular a GB.
de una semicircunferencia, con lo cual el segmento I será una altura del triángulo ya que es
perpendicular a GB.





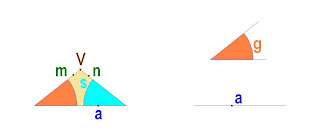
 Para construir un triángulo equilátero dada la altura h, hacemos primero un triángulo equilátero por el método anterior (dado un lado cualquiera MN perpendicular a h). A continuación marcamos la altura s en este triángulo y alineamos el vértice superior O de la altura s con el vértice superior O' de la altura dada h. Alineamos también el vértice J de la base del segmento dado s con el vértice de la base de h, esto es J'. En la intersección de las dos líneas a c obtenemos el vértice V, centro de la homotecia que transforma un triángulo en el otro: hacemos por J' una recta paralela a M N obteniendo la base del nuevo triángulo , en la intersección de esta recta con los dos rayos a, b, que son las líneas que pasan por V y MN obtenemos los vértices M'N'.
Para construir un triángulo equilátero dada la altura h, hacemos primero un triángulo equilátero por el método anterior (dado un lado cualquiera MN perpendicular a h). A continuación marcamos la altura s en este triángulo y alineamos el vértice superior O de la altura s con el vértice superior O' de la altura dada h. Alineamos también el vértice J de la base del segmento dado s con el vértice de la base de h, esto es J'. En la intersección de las dos líneas a c obtenemos el vértice V, centro de la homotecia que transforma un triángulo en el otro: hacemos por J' una recta paralela a M N obteniendo la base del nuevo triángulo , en la intersección de esta recta con los dos rayos a, b, que son las líneas que pasan por V y MN obtenemos los vértices M'N'.